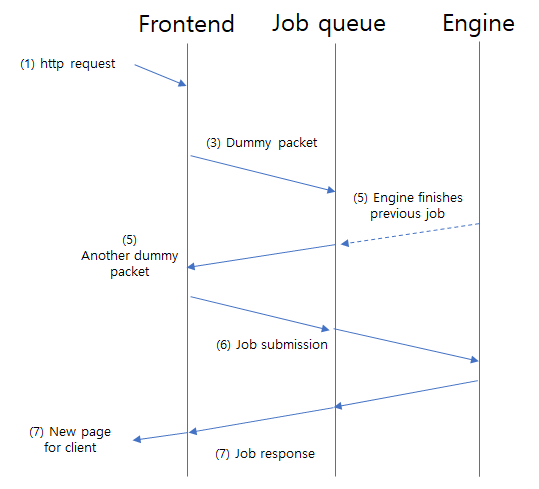
I opened this discussion: https://github.com/gcp/leela-zero/issues/2130
I was thinking a bit today and I think I will try implementing something that might be useful - disk-backed NNCache. Two usage cases that I can find useful would be:
- Use the cache file as an opening book - keep the NN eval results for the first 30 or so moves
- Pre-compute analysis : we can precompute the evaluation results for an sgf file overnight, and then use the precomputed NN eval results later for analyzing the game. The benefit is that the NN eval results will still be useful for playing variations of the sgf file.
With compression I think we can store tens of millions of eval results per GB - there are a couple of easy compression ideas since the NN eval result consists of a lot of zero or near-zero values.
On the cbaduk.net context, the main purpose is to cache the common opening sequences. Most of the compute load for Leela-zero is the neural net computation so anything that will make that part efficient will be an improvement.
So, what kind of problem are we facing?
The input of a NN evaluation is the current board state – the last eight states of the board, and whether the current player is black or white. The output of the net consists of 363 floating point numbers:
- (Policy) 362 for the probability of playing each move (0.0~1.0) – promising moves gets higher numbers while unlikely-to-be-useful moves gets near-zero.
- (Value) 1 for the probability of winning (-1.0~1.0)
363 floating point numbers x 4 bytes per number is roughly 1.5kB, which means caching a million moves will be 1.5GB. A single GTX 1080 can generate about 300 moves per second on a 40×256 net (the most complex nets) which means this will result in roughly 30GB every single day.
The dictionary probably has to grow in billions: Even if we only count 2 variations per move, the number of total combinations will quickly reach 2^30 (=1 billion) which will be 1.5TB – not only it is expensive to store but it also will require a lot of disk access. We probably will end up being slower than a GPU if we keep it in a single disk.
Luckily, we can cheat a bit:
- We are dealing with probabilities, and most of the 362 moves will be silly moves which will end up something close to zero.
- The NN results does not need to be precise. It’s not like we will pick one move over another because the probability changed to 60% from 85% – both are large enough to be most likely to be picked.
To put it simply, we can do a lossy compression.
How lossy can we go?
To see how lossy we can go, I devised an experiment – A 480-game match between four engines:
- (base) The baseline engine
- (quantize) An engine that quantizes the policy output into 256 discrete steps
x = static_cast<int>(x * 256);
x = x / 256;
- (quantize-sqrt) An engine that quantizes the policy output into 256 discrete steps after square-rooting it. What happens here is that the smaller numbers retain more accuracy while the larger numbers lose accuracy.
x = sqrt(x);
x = static_cast<int>(x * 256);
x = x / 256;
x = x * x;
- (quantize-pow2) An engine that quantize the policy output into 256 steps after doing a power-of-2. Over here the larger numbers retain accuracy while the smaller numbers still preserve them.
x = x * x;
x = static_cast<int>(x * 256);
x = x / 256;
x = sqrt(x);
…and here is the result:
A B C D
A base 38-42 33-47 58-22
B quantize 42-38 43-37 64-16
C quantize-sqrt 47-33 37-43 65-15
D quantize-pow2 22-58 16-64 15-65
What we can see here is that simply compressing the policy values into 256 steps is still good enough. However, for some reason, we lose strength when we lose information on the smaller values (quantize-pow2), while the larger values doesn’t seem to care much.
From now on, I will quantize the numbers into 2048 steps – this is 8x more steps than what we figured out that it is safe, but this is to avoid any unintended consequences, e.g., results going haywire when applied to a different net or a different board size.
What are we compressing?
To compress things effectively, the first thing to do is to see what kind of data is common and what is uncommon. To do so, I created the NN evaluation dumps from two self-play games, which consists of 487,883 evaluations. Then I quantized them into 2048 steps to see which values are the most common:
Value Count %
0 165614777 93.7724
1 3765003 2.13177
2 948082 0.536811
3 561482 0.317915
4 401759 0.227479
5 311689 0.176481
6 252915 0.143202
7 209827 0.118806
8 177416 0.100454
9 151993 0.0860596
Yes, 94 out of 100 values gets quantized to zero. This makes perfect sense since in any game most of the moves does not make sense. There usually are only a handful moves that makes any sense hence most of them will have extremely low probability. This means that the single most important scheme would be how we encode the large number of zeros.
Step 1 : Variable Length Coding
Since small values are likely to happen and large values are very unlikely, we can use different number of bytes to record them. So, here is the simple way:
- Value of 0 ~ 247 : write the value as a single byte as-is
- Value 248 ~ 2048 : The top 3 bits gets recorded on the LSB of the first byte, and the bottom 8 bits gets recorded on the next byte
So, basically something like this:
std::vector<std::uint8_t> ret;
for(auto x : in_array) {
int v = static_cast<int>(x * 2048.0);
if(v < 248) {
ret.push_back(v);
} else {
ret.push_back(248 + v / 256);
ret.push_back(v % 256);
}
}
return ret;
This resulted in an average of 363.921 bytes per encoding. Not bad considering that we started from 362 floating-point numbers (1440 bytes). This also shows that most of the values on the nets are less than 248 – to be exact, only 1.921 out of 362 are larger than 248 (or 0.12 before quantization)
Step 2 : Run Length Coding
We know that most of the values are zeros. So, rather than writing ‘zero zero zero zero …’. we can record zeros like ‘ten zeros’. So, we modify our encoding a bit more:
- Value of 0~239 : write the value as a single byte as-is
- Value 240 ~ 2048 : The top 3 bits gets recorded on the LSB of the first byte, and the bottom 8 bits gets recorded on the next byte. The first byte’s five MSBs are all ones.
- If we get N consecutive values of M (M is between 0 to 7) then the sequence gets recorded as (240+M, N). That is, seven consecutive zeros are recorded as (240, 7)
Here’s the code, a bit more complicated:
std::vector<uint8_t> ret;
int prev_value = -1;
int prev_cnt = 0;
for(auto x : xarray) {
int v = static_cast<int>(x * 2048.0);
if(prev_value == v && prev_cnt < 255) {
prev_cnt++;
} else {
if(prev_cnt > 0) {
if(prev_cnt == 1) {
ret.push_back(static_cast<uint8_t>(prev_value));
} else {
ret.push_back(static_cast<uint8_t>(prev_value + 240));
ret.push_back(static_cast<uint8_t>(prev_cnt));
runcount++;
runsum += prev_cnt;
}
}
prev_value = -1;
prev_cnt = 0;
if(v < 8) {
prev_value = v;
prev_cnt = 1;
} else if(v < 240) {
ret.push_back(v);
} else {
ret.push_back(248 + v / 256);
ret.push_back(v % 256);
}
}
}
if(prev_cnt > 0) {
if(prev_cnt == 1) {
ret.push_back(static_cast<uint8_t>(prev_value));
} else {
ret.push_back(static_cast<uint8_t>(prev_value + 240));
ret.push_back(static_cast<uint8_t>(prev_cnt));
runcount++;
runsum += prev_cnt;
}
}
return ret;
This time we got 52.215 bytes per encoding . Considering that we have one out of 17 values being zero, this means that we are going to have a lot of consecutive zeros which will all be reduced into 2 bytes.
Step 3 : Huffman Coding
We can see that there are some values (of the 256 possible values of a byte) going to be used frequently while others are going to be used infrequently. An ideal compression algorithm should result in every single possible being used fairly equally. So, what does the output distribution look like?
Value count %
...
---------------------
14 323995 1.27182
13 327487 1.28553
10 334606 1.31348
9 338045 1.32698
11 341306 1.33978
15 351303 1.37902
8 370494 1.45435
18 381949 1.49932
16 389688 1.5297
249 396717 1.55729
7 416312 1.63421
241 447475 1.75654
6 470702 1.84771
17 481525 1.8902
5 569659 2.23616
4 726237 2.8508
0 785929 3.08512
3 949443 3.72699
2 1722779 6.76267
1 2550610 10.0123
240 6550212 25.7125
Not good at all. 25% of them are 240 (consecutive zeros) and 10% are single ones. There are quite a bit of 241 (consecutive ones) and 249 (values larger than 256) but other than that, it’s just small numbers (0~16).
At this point, it seems that we can add more and more tricks or just use a more general solution – which i will continue on another post.